

Next: Univariate distributions
Up: Contents
Previous: Introduction
Activity 2.1
Why is
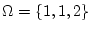
, not a sensible way to try to
define a sample space?

Answer 2.1
The proposed definition is not sensible, because the elements of
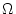
should all be different, but there are two elements 1 in
this proposed
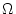
.

Activity 2.2
Write out all the events for the sample space
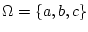
. (There are eight of them.)

Answer 2.2
The events are
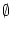
,
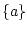
,
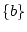
,
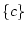
,
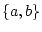
,
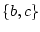
,
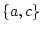
,
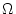
.

Activity 2.3
Prove, using only the axioms of probability given, that
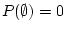
. (Hint:
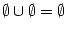
and
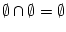
.)

Answer 2.3
Since
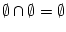
,
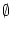
is
disjoint from
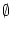
, we can apply the addition rule to get
which is
It follows by simple algebra that
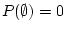
.

Activity 2.4
If all elementary outcomes are equally likely, and
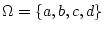
,
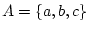
,
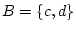
, find
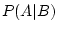
and
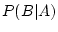
.

Answer 2.4
has 4 elementary outcomes that are equally likely, so
each elementary outcome has probability 1/4.

Activity 2.5
Identify the events and then the conditional probabilities
wrongly equated in the prosecutors fallacy above.

Answer 2.5
This is also an example of how slippery probability statements can
be when the outcome space is not well defined, and when they are
stated without care in ordinary language. How many readers of this
material thought that the prosecutor's argument was correct? And
yet it is an argument wholly lacking in coherence.
Let's imagine that for his first statement the prosecutor is
thinking about a large population of people similar to the
accused, say all men in the UK. The prosecutor's first statement,
based on the knowledge of the genetics of that population, is that
for a person taken at random from that population, the conditional
probability of a DNA match given that the person was not at the
crime scene is 1 in a million. We could write
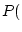
DNA match
Accused not at crime scene
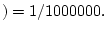
The prosecutor's next statement is that the probability of the
accused being at the crime scene given that there is a DNA match
is 1000000/1000001. We could write
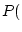
Accused at crime scene
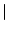
DNA match
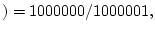
which is
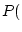
Accused not at crime scene
DNA match
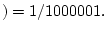
Its is clear that the prosecutor wants the jury to believe that
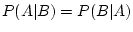
for event
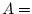
DNA match and event
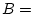
Accused not at crime scene. However, if
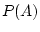
and
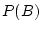
are different from each other, this equality will not be
true. The prosecutor wishes, in effect, that the jury treats
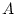
and
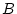
as the same event, but they are not the same.

Activity 2.6
Suppose that we toss a coin twice. The sample space is
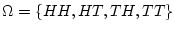
, where the elementary outcomes are
defined in the obvious way - for instance
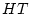
is heads on the
first toss and tails on the second toss. Show that if all four
elementary outcomes are equally likely, then the events `Heads on
the first toss' and `Heads on the second toss' are independent.

Activity 2.7
Show that if
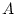
and
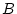
are disjoint events, and are also
independent, then
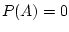
or
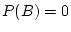
.

Answer 2.7
It's important to get the logical flow in the right
direction here. We are told that
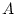
and
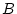
are disjoint events,
that is
So
We are also told that
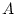
and
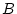
are independent, that is
It follows that
and so either
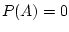
or
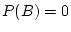
.

Activity 2.8
Prove this result from first principles.

Answer 2.8
From the definition of conditional probability we know
and that
It remains to show that
Now,
and using a distributive law for sets
Since the
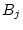
are disjoint events and
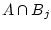
is included in
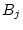
, the events
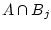
are disjoint. We can use the
addition rule for probabilities to get
It only remains to notice, as we did before, that from the
definition of conditional probability, for every
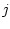

Activity 2.9
Plagiarism is a serious problem for assessors of course-work. One
check on plagiarism is to compare the course-work with a standard
text. If the course-work has plagiarised that text, then there
will be a 95% chance of finding exactly two phrases that are the
same in both course-work and text, and a 5% chance of finding
three or more. If the work is not plagiarised, then these
probabilities are both 50%.
Suppose that 5% of course-work is
plagiarised. An assessor chooses some course-work at random. What
is the probability that it has been plagiarised if it has exactly
two phrases in the text? And if there are three phrases? Did you
manage to get a roughly correct guess of these results before
calculating?

Answer 2.9
Suppose that two phrases are the same. We use Bayes' theorem.
Finding two phrases has increased the chance the work is
plagiarised from 5% to 9.1%. Did you get anywhere near 9% when
guessing?
Now suppose that we find three or more phrases.
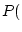
plagiarised
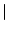
three the same
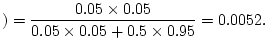
No plagiariser is silly enough to make three or more phrases the
same, so if we find three or more, the chance of the work being
plagiarised falls from 5% to 0.5%. How close did you get by
guessing?

Activity 2.10
A box contains three red balls and two green balls. Two
balls are taken from it without replacement. What is the
probability that 0 balls taken are red? And 1 ball? And 2 balls?
Show that the probability that the first ball taken is red is the
same as the probability that the second ball taken is red.

Answer 2.10
We have, in the notation used for sampling without
replacement,
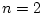
,
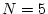
,
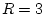
. The formula is
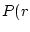
red
balls
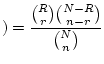
and so
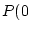
red
balls
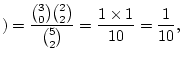
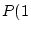
red
balls
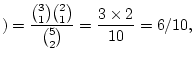
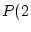
red
balls
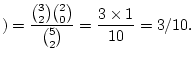
Note that these three probabilities must add to 1.
If the balls are labelled from 1 to 5, every possible permutation
of two of the numbers from 1 to 5 is an equally likely way in
which we can draw the first and second balls. Since each number is
equally often in first and second place in these permutations, the
number of red balls in first draws must be the same as the number
of red balls on second draws.



Next: Univariate distributions
Up: selftestnew
Previous: Introduction
M.Knott
2002-09-12
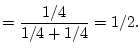
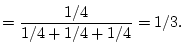
![]() and has
probability 1/2, for it is specified by two elementary outcomes.
The event `Heads on the second toss' is
and has
probability 1/2, for it is specified by two elementary outcomes.
The event `Heads on the second toss' is
![]() and has
probability 1/2. The event `Heads on both the first and the second
toss' is
and has
probability 1/2. The event `Heads on both the first and the second
toss' is
![]() and has probability 1/4. So the
multiplication property
and has probability 1/4. So the
multiplication property
![]() is
satisfied, and the two events are independent.
is
satisfied, and the two events are independent.
![]()
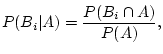
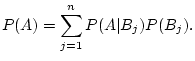
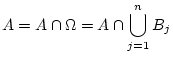
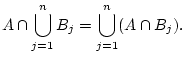
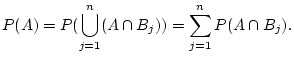
![]()
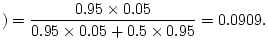
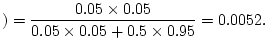
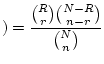
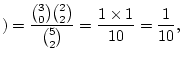
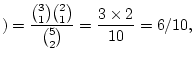
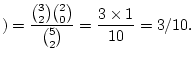
![]()