

Next: Bivariate distributions
Up: Contents
Previous: Probability
Activity 3.1
Show that for a discrete random variable
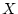
taking integer
values
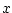
,
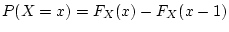
.

Answer 3.1
The event
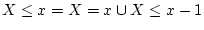
, and the two events on
the right are disjoint, so using the addition rule,
and this may be rewritten
which immediately gives the result wanted.

Activity 3.2
The greengrocer has a very large (effectively infinite) pile
of oranges on his stall. The pile of fruit is a mixture of 50%
old fruit with 50% new fruit; one can't tell which are old and
which are new. However, 20% of old oranges are mouldy inside, but
only 10% of new oranges are mouldy. Suppose that you choose 5
oranges at random. Is it true that the number of mouldy oranges in
your sample has a binomial distribution with
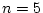
and
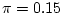
?

Activity 3.3
The chance that a lottery ticket has a winning number is
.0000001. If 10,000,000 people buy tickets that are independently
numbered, what is the probability of 0 winner? Of 1 winner?
(Hint, use a Poisson distribution with mean 1. The answers are 0.37, 0.37.)

Answer 3.3
We would expect in this case that the Poisson distribution would be a good
approximation to the binomial distribution with
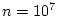
and
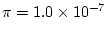
that would be be the natural distribution
to use. The approximation is good because
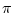
is very small and
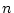
very large. The mean for the approximating Poisson
distribution is
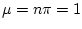
. From the Poisson Tables, Table 2 of the New Cambridge Statistical Tableswith
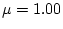
and
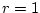
,
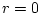
we get
So the probability of exactly 1 winner is
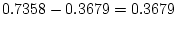
, and of exactly 0 winner is the same
as
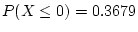
.
One could also use the probability function for the Poisson
distribution.
If we use the binomial distribution we get
The Poisson approximation is correct to at least 4 decimal places.
Notice that if one wanted, say,
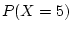
it would become difficult
to do the binomial calculation.

Activity 3.4
Show that for a uniform random variable on
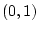
, if the
probability
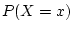
is the same for all
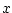
between 0 and
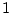
,
then it must be equal to 0 for all those
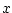
(otherwise the
probability of the sample space is not equal to
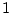
, but
infinite).

Answer 3.4
Suppose that
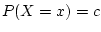
for
all choices of
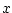
between 0
and 1. We can define a disjoint events
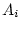
, for
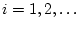
by
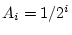
. From the second axiom of probability, for each
positive integer
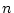
.
For each choice of
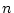
the probability on the left must, from the
first axiom of probability be less than or equal to 1, so that
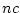
must be less than or equal to 1 for each choice of
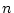
.
Unless
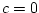
this is not true, because for each given
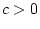
we can always choose
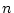
so large that
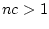
. For instance,
suppose we think that
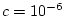
might do. It will not, because
by choosing
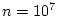
we would get
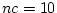
, and would have
constructed an event with probability greater than 1.

Activity 3.5
Suppose that
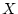
is uniformly distributed on
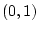
.
What
is
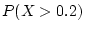
,
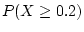
,
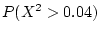
. (Hint: All these
probabilities are the same.)

Answer 3.5
We have
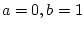
, and can use the formula for
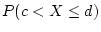
.

Activity 3.6
If
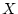
is a random variable with a standard normal
distribution, what is
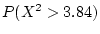
?

Answer 3.6

Activity 3.7
Show
that the mean of the exponential distribution is
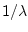
.

Answer 3.7
If
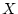
has density function
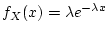
,
then the mean of
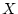
is

Activity 3.8
Find the mean of the Bernoulli trial
distribution, where
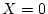
with probability
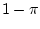
and
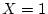
with
probability
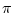
.

Answer 3.8
The mean of
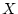
is

Activity 3.9
What is the expected value of
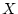
if the only possible value
of
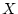
is 0? (We have
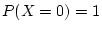
, so
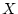
is effectively a
constant, even though it is called a random variable.)

Answer 3.9

Activity 3.10
Show, that
![$ E[X-E(X)]=0$](img148.png)
.

Answer 3.10
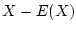
is the sum of two random variables
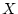
and the degenerate
random variable
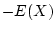
that takes the value
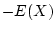
with
probability 1. so,

Activity 3.11
Show that the
variance of the Bernoulli trial distribution is
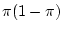
.

Answer 3.11
We know already that
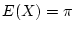
, and
So
![$ \operatorname{var}X=E(X^2)-[E(X)]^2=\pi-\pi^2=\pi(1-\pi)$](img155.png)
.

Activity 3.12
Show that if
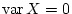
then
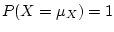
. (We say in
this case that
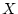
is
almost surely equal to its
mean.)

Activity 3.13
Find the variance of the exponential distribution with mean
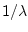
.

Answer 3.12
We know already that
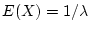
.
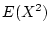
is
So the variance is
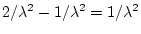
.



Next: Bivariate distributions
Up: selftestnew
Previous: Probability
M.Knott
2002-09-12
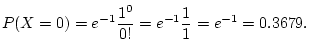
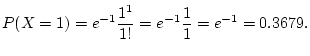
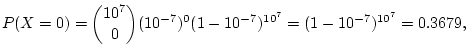
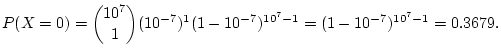
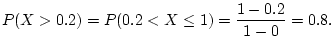
![$\displaystyle \int_0^\infty x\lambda e^{-\lambda x}dx=[-xe^{-\lambda x} -
e^{-\lambda x}/\lambda]^\infty_0 = 1/\lambda.
$](img141.png)
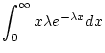
![$\displaystyle =[-x^2e^{-\lambda x}]^\infty_0 +2\int_0^\infty xe^{-\lambda x}dx$](img161.png)
![$\displaystyle = [-x^2e^{-\lambda x}-2xe^{-\lambda x}/\lambda ]^\infty_0+ 2\int_0^\infty e^{-\lambda x}/\lambda$](img162.png)