

Next: Sampling distributions
Up: selftestnew
Previous: Univariate distributions
Activity 4.1
How would the scatter diagram change if the random variables
were discrete rather than continuous?

Answer 4.1
If the random variables are discrete, there will be a possibility
of many points at the same place in the scatter diagram. For
instance, if both
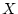
and
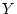
take only positive integer values,
we might get several observations with
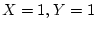
, leading to
several points at
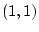
. The coincident points are hard to
represent adequately in the scatter diagram. Sometimes a bigger
dot is used when there are several points.

Activity 4.2
Write down the marginal distribution of
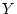
, and the
conditional distributions of
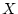
given
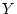
.

Answer 4.2
The marginal distribution of
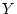
is found from the column totals.
The conditional distribution of
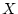
for
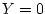
is found by dividing
the probabilities in the first column by the first column total.
The conditional distribution of
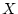
for
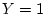
is found by dividing
the probabilities in the second column by the second column total.
The conditional distribution of
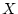
for
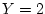
is found by dividing
the probabilities in the third column by the third column total.
In fact, we know for sure that
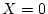
if
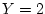
.

Activity 4.3
Nothing in principle stops us from thinking about the joint
distribution of
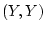
, though this is a fairly pointless thing
to do except for consistency of approach. From the last definition
of
, write down the table of probabilities for
the joint distribution
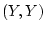
.

Answer 4.3
Table 4.1:
Probabilities for joint distribution of 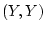
| |
|
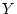 |
| |
|
0 |
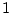 |
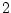 |
| |
0 |
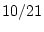 |
0 |
0 |
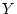 |
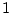 |
0 |
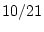 |
0 |
| |
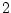 |
0 |
0 |
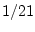 |

Activity 4.4
Why isn't (4.1) any good for continuous variables?

Answer 4.4
For continuous random variables
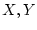
,
![$ P[X=x,Y=y]=0$](img191.png)
and
![$ P[X=x]=0$](img192.png)
,
![$ P[Y=y]=0$](img193.png)
. So for continuous variables,
![$ P[X=x,Y=y]=P[X=x]P[Y=y]$](img194.png)
for all
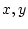
whether or not there is
independence for
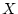
and
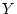

Activity 4.5
Show that if
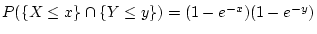
for all
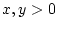
, then
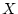
and
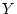
are
independent random variables, each with an exponential
distribution. (Hint: use (4.2).)

Answer 4.5
The righthand side of the result given is the product of the cdf
for an exponential random variable
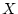
with mean 1 and the cdf for
an exponential random variable
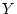
with mean 1. So the result
follows from (4.2).

Activity 4.6
There are other ways to write the covariance. Show that
and

Answer 4.6
The remaining result follows by an argument symmetric with the
last one.

Activity 4.7
Suppose that
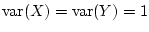
, and that
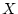
and
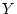
have
correlation coefficient
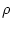
. Show that it follows from
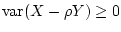
that
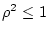
.


 Next: Sampling distributions
Up: selftestnew
Previous: Univariate distributions
M.Knott
2003-11-05
Next: Sampling distributions
Up: selftestnew
Previous: Univariate distributions
M.Knott
2003-11-05