Interval estimation

Activity 7.1   Justify the last statement.
$\blacksquare$

Answer 7.1   We just have to rework the inequality. Going step by step:

$$P\left[\left\vert\frac{\bar{X}-\mu}{1/\sqrt{n}}\right\vert\le 1.96\right] =0.95$$

$$P\left[-1.96/\sqrt{n}\le \bar{X}-\mu\le 1.96/\sqrt{n}\right] =0.95$$

$$P\left[-1.96/\sqrt{n}-\bar{X}\le -\mu\le -\bar{X} +1.96/\sqrt{n}\right] =0.95$$

$$P\left[1.96/\sqrt{n}+\bar{X}\ge \mu\ge \bar{X} -1.96/\sqrt{n}\right] =0.95$$

$$P\left[\bar{X}-1.96/\sqrt{n}\le \mu\le \bar{X} +1.96/\sqrt{n}\right] =0.95$$

$\blacksquare$

Activity 7.2   Why don't we always choose a very high confidence for the interval?
$\blacksquare$

Answer 7.2   We don't always want to use a very high confidence, because the interval would be very long. We have to trade off the length of the interval against the confidence percentage.
$\blacksquare$

Activity 7.3   Prove the last statement.
$\blacksquare$

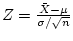
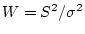
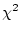
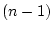
Answer 7.3   We know that $Z=\frac{\bar{X}-\mu}{\sigma/\sqrt{n}}$ has a standard normal distribution, and that $W=S^2/\sigma^2$ has an independent $\chi^2$ distribution with $(n-1)$ degrees of freedom. It follows that

$$\frac{Z}{\sqrt{W/(n-1)}}=\frac{\bar{X}-\mu}{S/\sqrt{n}}$$

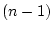
has a Student's t distribution with $(n-1)$ degrees of freedom.
$\blacksquare$

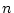
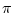
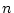
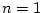
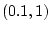
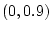
Activity 7.4   The results in (7.10) work only for large $n$, and $\pi$ not too close to 0 or to 1. If $n$ is very small then it becomes more difficult to obtain intervals with approximately a 95% confidence. Show that if $n=1$, and we use the confidence interval $(0.1,1)$ when there is a success, and $(0,0.9)$ when there is a failure, we attain confidence of at least 90%, though the actual confidence percentage achieved varies with the true value $\pi$.
$\blacksquare$

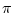
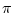
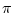
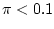
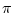
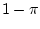
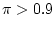
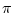
Answer 7.4   If $\pi$ is between 0.1 and 0.9, our interval always covers $\pi$, so for these values the probability of coverage is 100%. This is certainly greater than 90%. If $\pi < 0.1$ then the probability of covering $\pi$ is the probability that there is a failure, which is $1-\pi$, which is therefore greater than or equal to 90%. 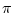Similarly, if $\pi >0.9$, the probability of covering $\pi$ is the probability that there is a success, which is $\pi$, which is greater than 90%.
$\blacksquare$