Hypothesis testing

Activity 8.1   Why does it make no sense to use a hypothesis like $\bar{x}=2$?
$\blacksquare$

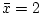
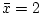
Answer 8.1   We can see immediately if $\bar{x}=2$ by calculating the sample mean. Inference is concerned with the population from which the sample was taken. We are not very interested in the sample mean in its own right.
$\blacksquare$

Activity 8.2   Of 100 clinical trials, 5 have shown that wonder-drug zap2 is better than the standard treatment (aspirin). Should we be excited by these results?

Of the 1000 clinical trials of 1000 different drugs this year 30 trials found drugs that seem better than the standard treatments with which they were compared. The television news reports only the results of those 30 `successful' trials. Should we believe the television news reports?

A child welfare officer says that she has a test that always reveals when a child has been abused, and she suggests it be put into general use. What is she saying about Type I and Type II errors for her test?
$\blacksquare$

Answer 8.2   If 5 clinical trials out of 100 report that zap2 is better, that is consistent with there being no difference whatsoever between zap2 and aspirin and a 5% Type I error being used for tests in those clinical trials. With a 5% level of significance we expect 5 trials in 100 to show spurious significant results.

If the news reports the 30 successful trials out of 1000, and those trials use tests with significance level 5%, we may well choose to be very cautious about believing the results. We would expect 50 spurious significant results in the 1000 trial results.

The welfare officer is saying that the Type II error has probability zero. The test is always positive if the null hypothesis of no abuse is false. On the other hand, the welfare officer is saying nothing about the probability of Type I error. It may well be that the probability of Type I error is high, which would lead to many false accusations of abuse when no abuse had taken place. One should always think about both types of error when proposing a test.
$\blacksquare$

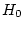
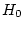
Activity 8.3   You should be able to verify that for each of these critical regions the probability of rejecting $H_0$ when $H_0$ is true is $100\alpha$%.
$\blacksquare$

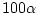
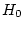
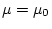
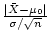
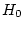
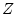
Answer 8.3   When $H_0$ is true, $\mu=\mu_0$, and so $\frac{\vert\bar{X}-\mu_0\vert}{\sigma/\sqrt{n}}$ has a standard normal distribution. The probability of rejecting $H_0$ is then the probability of a standard normal random variable $Z$ taking values in both tails, the left hand tail, or the right hand tail respectively. It is easily seen that all the probabilities are $\alpha$.
$\blacksquare$

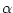
Activity 8.4   Why don't we use a two-tailed test for a one-sided Alternative Hypothesis?
$\blacksquare$

Answer 8.4   We do not use a two-tailed test for a one-sided alternative hypothesis, because the two-tailed test would have a greater probability of Type II error. It would have less power.
$\blacksquare$

Activity 8.5   There is no obvious link between confidence intervals and one-tailed tests. What sort of confidence interval would one need to define to have such a link?
$\blacksquare$

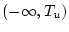
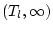
Answer 8.5   One would need to have confidence intervals of the form $(-\infty, T_u)$, and $(T_l,\infty)$. The first type would just give, say, 95% confidence that $\theta \le T_u$.
$\blacksquare$

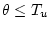
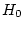
Activity 8.6   Suppose that we have two independent samples from normal populations with known variances. We want to test the null hypothesis that the two populations have the same mean against the alternative that the means are different. One could use each sample by itself to write down a 95% confidence interval for the corresponding population mean. One could reject $H_0$ if those intervals did not overlap. What would be the significance level of this test?
$\blacksquare$

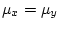
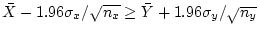
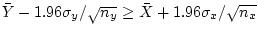
Answer 8.6   Let us assume the Null Hypothesis is true, and that $\mu_x=\mu_y$. The two intervals do not overlap if and only if $\bar{X}-1.96\sigma_x/\sqrt{n_x} \ge \bar{Y}+1.96\sigma_y/\sqrt{n_y}$ or $\bar{Y}-1.96\sigma_y/\sqrt{n_y} \ge \bar{X}+1.96\sigma_x/\sqrt{n_x}$. So we want the probability

$$P[\vert\bar{X}-\bar{Y}\vert\ge 1.96(\sigma_x/\sqrt{n_x}+\sigma_y/\sqrt{n_y})]$$

This is

$$P[\frac{\vert\bar{X}-\bar{Y}\vert}{\sqrt{\sigma^2_x/n_x+\sigma^2_... ...igma_x/\sqrt{n_x}+\sigma_y/\sqrt{n_y}}{\sqrt{\sigma^2_x/n_x+\sigma^2_y/n_y}}].$$

We have constructed a standard normal random variable, so the probability is

$$P[\vert Z\vert\ge 1.96\frac{\sigma_x/\sqrt{n_x}+\sigma_y/\sqrt{n_y}}{\sqrt{\sigma^2_x/n_x+\sigma^2_y/n_y}}].$$

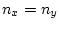
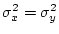
This does not reduce in general, but if we assume $n_x=n_y$ and $\sigma^2_x=\sigma^2_y$, then it reduces to

$$P[\vert Z\vert\ge 1.96\sqrt{2}]=0.0056.$$

So the significance level is about 0.6%, which is much smaller than the usual conventions of 5% or 1%. Putting variability into two intervals makes them more likely to overlap than you might think, and so your chance of wrongly rejecting the Null Hypothesis is smaller than you might expect.
$\blacksquare$