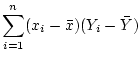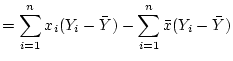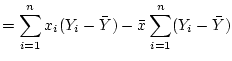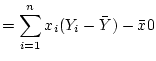

Next: Simple linear regression
Up: Contents
Previous: Analysis of variance
Activity 10.1
Looking at the figure, would you expect that
estimates of the regression based purely on the observed points
would be close to the population line, or far away?

Answer 10.1
The random samples show in every diagram points that lie
very close to the population regression line. One would expect for
this population that any reasonable estimation method would be
able to provide a good estimate.

Activity 10.2
The Figures
show the same set of 15 points fitted by a variety of straight
lines. In the first figure the lines go through the centre of
gravity but have varying slopes. In the second figure the lines
have something not too far off the right slope, but they don't all
go through the centre of gravity of the observations. The line
that fits best according to the least squares principal is the one
that minimises the sum of the squared lengths of the little black
vertical lines that join the observations to the fitted values.
Working by eye, choose the best lines in the two Figures.

Answer 10.2
For the first Figure the best fit is from the first
diagram in the second row. For the second Figure the best fit
is probably also the first one in the second row.

Activity 10.3
Suppose that we miss out the
observation
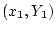
, and recalculate the slope estimate
.
Find a formula for the difference between the old and new slope
estimates. Check it works for
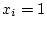
, all
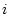
.

Answer 10.3
The original estimator must be corrected by taking off the
weighted contribution of the first observation, and then adjusting
the total weight. So if the original estimator is
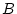
, the new
one is
The difference between
and the new estimate is
which is a rather simple multiplier of the residual at the first
observation in the original model.
If 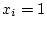 for all
for all 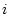 , then
, then 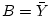 and the difference
becomes
and the difference
becomes
This is easily checked to be the difference between the mean
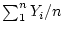
and the mean
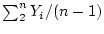
.

Activity 10.4
Show that
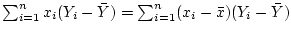
and that
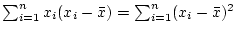
.

Answer 10.4
The other one is just the same, except one must replace
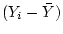
everywhere by
.



Next: Simple linear regression
Up: selftestnew
Previous: Analysis of variance
M.Knott
2002-09-12
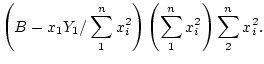
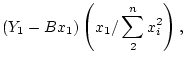
![]() for all
for all ![]() , then
, then ![]() and the difference
becomes
and the difference
becomes