Answer 11.1
For a regression line through the origin,
where
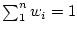
. First the expected value:
So, the estimator of slope is unbiased. Now for the variance:

Answer 11.2
When
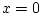
the fitted value become the intercept
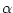
,
so the results should be the same.

Answer 11.4
For the first case, when the regression is quadratic, the
model that says the regression is linear is clearly wrong.
If there is some increase in variation around the regression line
with 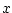 , then the assumption that the error variance is the same
for each observation must be wrong.
, then the assumption that the error variance is the same
for each observation must be wrong.
If there s a wild observation, then that observation does not
follow the model at all, so the model does not hold for all the
observations.

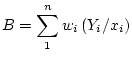
![$\displaystyle = E[\sum_1^nw_i\left(Y_i/x_i\right)]$](img343.png)
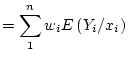
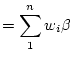
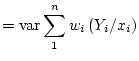
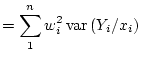
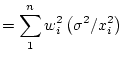
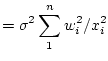
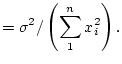
![]() , then the assumption that the error variance is the same
for each observation must be wrong.
, then the assumption that the error variance is the same
for each observation must be wrong.
![]()