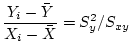Correlation

Activity 12.1   Show that if $R_{xy}^2 = 1$, then $(X_i, Y_i)$ all lie exactly on a straight line.
$\blacksquare$

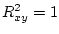
Answer 12.1   If $R_{xy}^2 = 1$, then there is also equality in the original inequality, so we must have

$$(X_i-\bar{X})-S_{xy}(Y_i-\bar{Y})/S_y^2=0$$

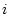
for every $i$. This gives

$$\frac{Y_i-\bar{Y}}{X_i-\bar{X}}=S_y^2/S_{xy}$$

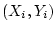
and so all the points $(X_i, Y_i)$ lie on a straight line through $(\bar{X},\bar{Y})$ with slope $S_y^2/S_{xy}=S_{xy}/S_x^2$.
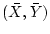
$\blacksquare$

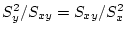
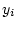
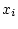
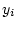
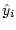
Activity 12.2   Why is the squared sample correlation coefficient between the $y_i$s and $x_i$s the same as the squared sample correlation coefficient between the $y_i$s and $\hat{y}_i$s? No algebra is needed for this.
$\blacksquare$

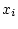
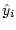
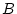
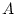
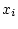
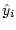
Answer 12.2   The only difference between the $x_i$s and $\hat{y}_i$s is a rescaling by multiplying by $B$, followed by a relocation by adding $A$. Correlation coefficients are not affected by a change of scale or location, so it will be the same whether we use the $x_i$s or the $\hat{y}_i$s.
$\blacksquare$