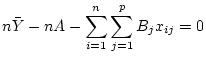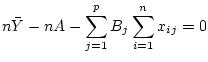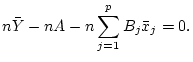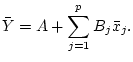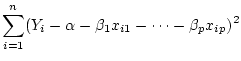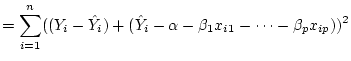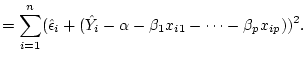Answer 13.1
The equation
may be written
which on summing through the bracket gives
Interchanging the order of the sums,
which gives
Dividing by
shows that
The last equation is the result asked for.

Answer 13.2
For any choice of
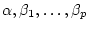
, we have
Now we can square the two terms in the main bracket and carry
through the sum. The least squares equations give immediately that
the cross-product term vanishes because
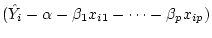
has terms which do not vary with
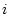
or vary with
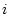
only through the presence of
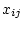
.

Activity 13.3
Suppose that
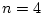
the values for
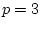
explanatory
variables are in the columns
Answer 13.3
One should just do the two calculations for each row of the
table. For instance, in row 1,
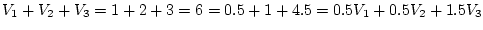
. There is
collinearity here, since
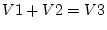
.

Activity 13.4
If the model fits, then the fitted values and the residuals
from the model are independent of each other. What do you expect
to see if the model fits when you plot residuals against fitted
values?

Answer 13.4
If the model fits, one would expect to see a random scatter
with no particular pattern.


 Next: Tests for goodness-of-fit
Up: selftestnew
Previous: Correlation
M.Knott
2002-09-12
Next: Tests for goodness-of-fit
Up: selftestnew
Previous: Correlation
M.Knott
2002-09-12
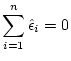
![$\displaystyle \sum_{i=1}^n \left[Y_i- A - \sum_{j=1}^pB_jx_{ij}\right]=0
$](img367.png)